目次
平和『ルパン三世Lupin The End(1/319ver)』10月23日リリース決定!
ついに新本命が姿を現しました!スペックを徹底的に解析完了であります!
今まで幾つかのPVで煽ってきましたが、やっと全貌が見えてきました。
スペックはもちろん新MAXですが、予想通りの確変ループです。
確変ループを『正統派』なんて言っちゃってますが、そこまでSTのルパンを否定しなくても…なんて思ったりもします。
いったいどんなスペックに仕上がっているのか、早速見ていきましょう!
【スペック解析】
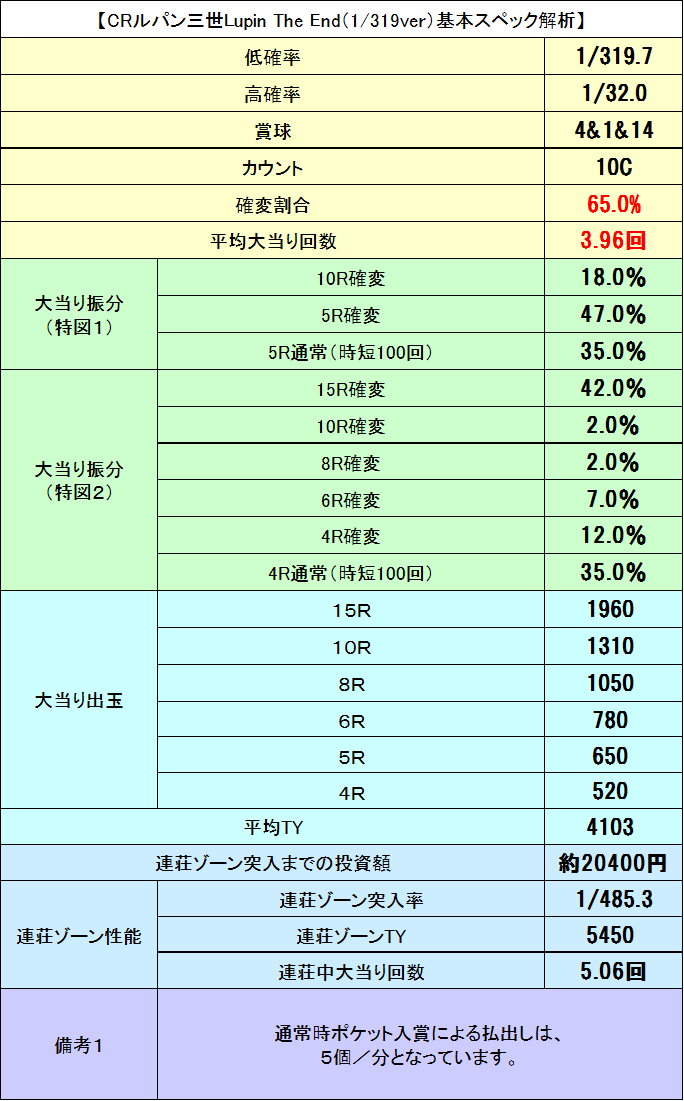
初当り確率1/319の65%確変ループタイプです。
まず初当りですが、目を引くのは非確変の時短です。
今までは20回とか40回とか少ない時短しか付けてくれない平和さんでしたが、ついに時短100回搭載です!
ガルパンで学習してくれたんですよね、きっと…
初当りは5Rが基本となりますが、時短100回付加されていることにより、連チャンモード突入率が上がっています。
確変割合65%ですから、
連チャンモード突入率は、約74.4%!
この高さは、まだ勢いのあるV-STタイプと差別化が出来てるので、好印象だと思います。
そして連チャンモードですが、消されたルパンを意識しているため、
- MAX大当りは2000発以上
- ランクアップボーナス搭載
- バトルスペック仕様
以上の3点は欠かせないものとなっていますね。
65%継続率規制があるため、最低の4Rが確変と通常合わせて47%もあるのは微妙と感じてしまいますが、42%占める15Rがどこまで爆発してくれるかが勝負となりそうです。
継続率については、初当りと同じ65%確変+通常大当りに時短100回となるため、
連チャンモード継続率も、約74.4%!
時短での引戻しがかなりアツいことになりそうですね!
【ハマリ&連チャン徹底解析!】
1/319などと現行MAXのハマリをナメたらいけない!
逆に噴射する時は2000発の連打!
新生ルパンのハマリと連チャンを徹底解析!
⇒⇒連チャン性能&ハマリ性能を徹底解析!『ルパン三世Lupin The End(1/319ver)』
【一撃連チャン爆発力勝負!】
同じ週で導入となる『牙狼闇を照らす者』と未だ人気を誇る『蒼天の拳』との三つ巴!
一体どの機種が爆発力を制するのか!?
⇒⇒【パチンコ】『ルパン三世Lupin The End(1/319ver)』一撃連チャン爆発力勝負!
【ボーダーライン&期待値解析】
全国で広がる非等価の流れにしっかり対応!
北海道・東北エリア・東京・関西エリアを中心とする『27.5玉交換』と、中部エリア・中四国エリア・九州エリアを中心とする『28玉交換』をばっちり網羅!
さらに1パチのボーダーライン&期待値もガッツリ対応済です。
⇒⇒【パチンコ】『ルパン三世Lupin The End(1/319ver)』ボーダー全解剖!
【『消されたルパン』を本当に超えることは出来るのか?】
これはいろんな人から寄せられる質問です。
正直に答えるならば、超えることは難しいと思います。
そもそも消されたルパンは確変82%の高継続だったからこそ、あのバトルが成り立っていたと思うからです。
確かに今回もトータルの継続率は74%と高いものの、それは時短を含めての話です。
この時短というのは、バトル敗北後での展開ですから、
『連チャンするけど銭形に負けてばかり…』
という構図になるのは目に見えています。
それでも新しいゲーム性にチャレンジしなかったのは、きっとチャレンジできなかったから。
メーカーの視点から見ると、ルパンは絶対に不人気で終わらせてはいけないモチーフですから、過去の栄光に頼らざるを得なかったのではないかと思います。
しかし、だからといってそこまで悲観的になることはないかな、とも一方で思うのです。
もう82%だなんて継続率は今後リリースできませんし、時代によって今までもいろんなシガラミを超えてきました。
だからこそ、新生ルパンとして、ちょっと気持ちをリセットして勝負するのが良いのではないかなと思います。
今回はいろんなギミックを搭載していますし、平和さんのことですから、消されたルパンにはなかった楽しみ方をギュッと入れ込んでくれているはず!
導入は10月後半ということですから、あと2ヶ月きりましたね。楽しみにしたいと思います!
【まとめ】
- 新ルパンは王道確変ループタイプ!
- 初当りにも確変65%+時短100回つくため、連チャンモードに突入しやすい!
- 一撃性能はちょっと控えめだが、15Rを引けるかが勝負!
- 正直『消されたルパン』は超えられない…でも新しい楽しみ方があるはず!